재밌고 어려운 IT를 이해해보자~!
이진 탐색(Binary Search) 본문
이진 탐색(Binary Search)의 개념
정렬되어 있는 데이터에서 원하는 값을 찾아내는 탐색 알고리즘 입니다.
이진 탐색은 이분탐색이라고도 불리며 정렬된 데이터에서 탐색구간을 반복적으로 반으로 줄여나가며 원하는 값을 찾아 내는 방식으로 동작합니다. 주로 배열에서 사용되며 리스트, 트리 자료구조에서도 사용이 가능합니다.
주의점!
이진 탐색을 사용할 때에는 반드시 배열 내의 데이터가 오름차순 또는 내림차순으로 정렬되어 있어야 합니다.
보통의 경우 '오름차순으로 정렬된 데이터' 를 사용합니다. (정렬의 방향에 따라 탐색 범위를 좁혀가는 방향이 다르다)
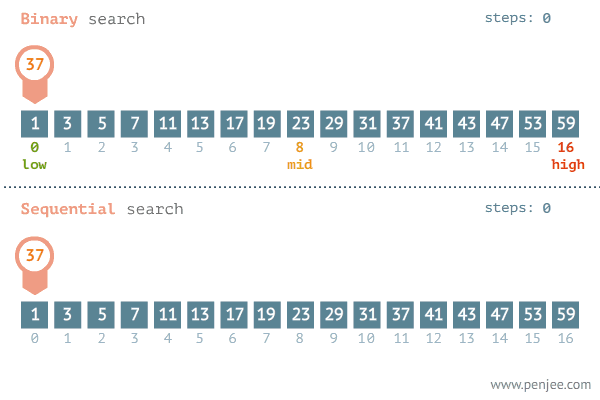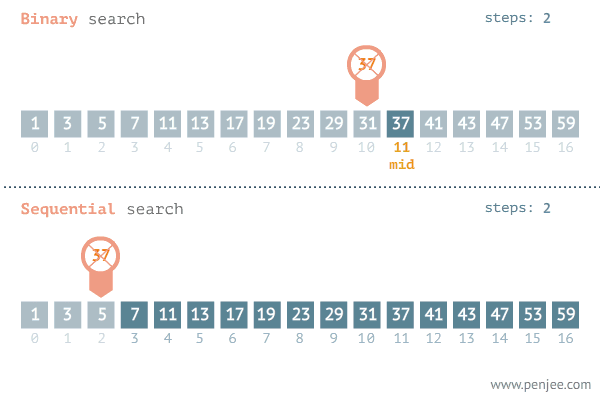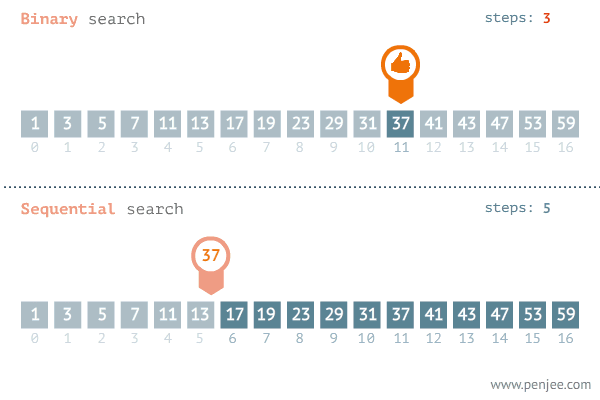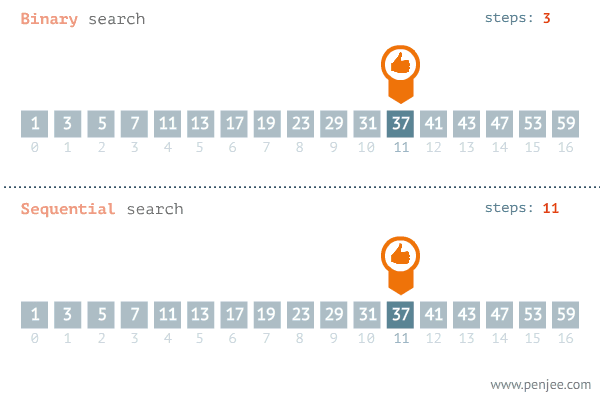
이진 탐색의 목적
이진 탐색의 목적은 데이터 양이 무수히 많을 때 원하는 값을 빨리 찾기 위한 것이 목적입니다.
검색 대상의 크기와 상관없이 빠른 검색 속도를 제공한다는 것으로, 검색 대상이 매우 큰 경우에도 탐색 시간이 빠르기 때문에, 대량의 데이터를 다루는 알고리즘에서 많이 사용됩니다.
이진 탐색 구현
1. 오름차순으로 정렬된 배열 array 생성
array의 시작 인덱스 0 은 low
array의 마지막 인덱스 array.length-1 은 high 로 지정.
2. low와 high의 중간인덱스 mid 계산
mid = ( low + high ) / 2
3. key값 (원하는 값) 을 입력받고 mid보다 작은지, 큰지 확인 후 탐색 구간 재설정
if key == array[mid] ---> 종료 (원하는값 찾음)
if key < array[mid] ---> 원하는 값이 중간값 보다 낮다면 high를 mid-1로 설정하고 mid 재 계산. 우측을 전부 버린다.
if key > array[mid] ---> 원하는 값이 중간값 보다 높다면 low를 mid+1로 설정하고 mid 재 계산. 좌측을 전부 버린다.
4. 최종적으로
원하는 값을 찾을 떄 까지 반복

한글 코딩
한글 코딩
오름차순 배열생성
lowidx = 시작인덱스
highidx = 마지막인덱스
배열 출력
유저한테 원하는 값 입력받기 (key값)
while (시작인덱스가 마지막인덱스보다 작거나 같을때까지) {
//중간인덱스
mididx = (시작인덱스+마지막인덱스))/2; //찾는 범위를 반복적으로 재설정 해줘야 하기 때문에 while문 안에 작성
if ( 원하는값 == 중간값 ) {
찾는값과 찾는값의 인덱스 출력 후
종료
}
else if ( 원하는값 < 중간값 ) {
마지막인덱스 = 중간인덱스 -1;
}
else if ( 원하는값 > 중간값 ) {
시작인덱스 = 중간인덱스 +1;
}
이진 탐색 코드
package teamam;
import java.util.Scanner;
public class Binarysearch {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//오름차순 배열 생성
int[] array = new int[8];
array[0] = -9;;
array[1] = -4;
array[2] = 0;
array[3] = 10;
array[4] = 38;
array[5] = 50;
array[6] = 100;
array[7] = 1300;
//이진 탐색을 위한 시작 인덱스, 마지막 인덱스 선언 및 대입
int lowIdx = 0;
int highIdx = array.length-1;
// 배열 출력 및 찾는 값 입력
System.out.print("[ ");
for (int arrdata : array) {
System.out.print(arrdata+" ");
}
System.out.println("]");
System.out.println("다음 배열중 찾으시는 값을 입력하세요.");
int key = sc.nextInt(); //찾고자 하는 값 입력
boolean keynotfound = true; //값을 찾았을때 "찾는 값이 없습니다" 를 출력 안하기 위해 체크하는 변수
while (lowIdx <= highIdx) { //low인덱스가 high인덱스보다 작거나 같을때 까지 반복
// low, high 인덱스가 바뀔 때 마다
//중간인덱스를 계속 재설정 해서 탐색 범위를 좁혀나간다.
int midIdx = (lowIdx + highIdx)/2;
if (key==array[midIdx]) { //원하는값 == 중간값 이면 종료
System.out.println("찾으시는 값 : "+array[midIdx]+"\n찾으시는 값의 인덱스 : "+midIdx);
keynotfound = false;
break;
}
else if (key>array[midIdx]) { //원하는값이 중간값보다 크면
lowIdx = midIdx+1; // 중간값인덱스 +1을 시작인덱스에 대입.
}
else if (key<array[midIdx]) { //원하는값이 중간값보다 작으면
highIdx = midIdx-1; // 중간값인덱스 -1을 마지막인덱스에 대입.
}
}
if (keynotfound) {
System.out.println("찾는 값이 없습니다.");
}
}
}
디버깅 표
- 배열에 있는값을 찾을 때 디버깅 표

- 배열에 없는 값 찾을 때 디버깅 표

따라서 원하는 값을 찾았을 떄는 break문으로 종료시킵니다.
원하는 값을 찾는 과정

시간복잡도 / 공간복잡도
어떤 알고리즘이 있을 때, 그 알고리즘의 성능 평가는 어떻게 할 수 있을까요?
알고리즘 성능을 평가하기 위해 '복잡도(Complexity)'의 척도를 사용한다고 합니다.
1. 시간복잡도
- 알고리즘이 실행되어 종료될 때까지 어느 정도의 시간이 필요한지 측정하는 방법.
- 실제 컴퓨터의 실행 시간을 측정하기는 어렵기 때문에 알고리즘의 실행문이 몇 번 실행되는지 횟수를 표시하여 측정.
- 빅오 표기법

2. 공간복잡도
- 알고리즘이 문제를 해결하는 데 어느 정도의 저장 공간을 필요로 하는지 측정하는 방법.
- 기억 장치 내의 공간을 얼마나 적게 사용하는지가 중요.
- 저장 공간은 알고리즘이 사용하는 공간과 알고리즘에 입력되어 처리되는 자료 공간을 모두 포함.

이진탐색의 시간복잡도 공간복잡도
이진탐색의 시간복잡도는 빅오표기법으로 O(log n)이며 이것은 다른 탐색에 비해서 매우 빠릅니다.
이진탐색의 공간복잡도는 기존에 주어진 배열에서 이루어지기 떄문에 O(1) 입니다.

실생활 이진탐색 적용
이진 탐색은 정렬된 자료구조에만 사용할 수 있다는 단점이 있지만, 검색이 반복될 때마다 검색 범위가 절반으로 줄기 때문에 속도가 빠르다는 장점이 있습니다. 따라서 방대한 양의 데이터가 있는 곳이라면 이진탐색이 사용되는 편 입니다.
1. 사전에서 단어찾기, 서점에서 책 찾기, 컴퓨터내에서 파일찾기 같은곳에 이진 탐색이 활용됩니다.
2. 맞히기 게임과 같이 정렬된 데이터속에 주어진 범위내에서 뭔가 맞춰야할떄 활용됩니다.
*참조
https://minhamina.tistory.com/127
https://adjh54.tistory.com/187
https://computer-engineering.tistory.com/2
https://blog.penjee.com/binary-vs-linear-search-animated-gifs/
'코리아IT핀테크과정' 카테고리의 다른 글
| 함수(Function) (0) | 2023.11.27 |
|---|---|
| 버블정렬 코드 개선 (0) | 2023.11.27 |
| 학생부 프로그램 제작 (2) | 2023.11.25 |
| 배열(Array) (3) | 2023.11.23 |
| 형변환, 반복문 (0) | 2023.11.22 |



